[알고리즘] 병합정렬(Merge Sort) (Python)

1. 기본 원리

• 리스트를 절반으로 나누는 함수를 재귀적으로 활용하면서 원소가 하나인 상태까지 잘게 나눠줌
• 나눠진 부분들을 정렬해나가며 하나씩 붙여나감

 

2. 생각정리

• [2,8,6,5,1]를 병합정렬로 정렬하는 시뮬레이션을 돌려봤습니다.

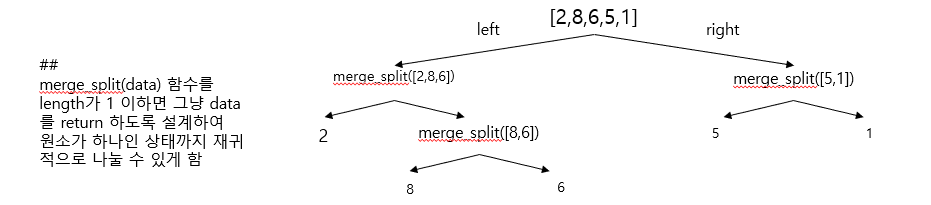
나누는 과정

다 나눠지면 left와 right을 merge 하는 과정을 통해

합치기(1)

합치기(2)

합치기(3)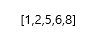

합치기(4)

 

3. 코드 구현

음... 솔직히 어떤 방식으로 정렬을 진행하는지는 개념적을 쉽게 이해가 되었는데...

재귀적으로 구현하려고 하니까 바로 이해가 안되었던 것 같습니다.

분할하는 프로세스를 '내려간다고' 표현하고

합치는 프로세스를 '올라간다고' 표현하면

가장 밑바닥을 찍은 순간 바로 올라갈 수 있는 함수가 작동하게? 코드를 짰습니다.

def merge(left, right):
    merged = list()
    left_point, right_point = 0, 0
    
    # case1 - left/right 둘다 있을때
    while len(left) > left_point and len(right) > right_point:
        if left[left_point] > right[right_point]:
            merged.append(right[right_point])
            right_point += 1
        else:
            merged.append(left[left_point])
            left_point += 1

    # case2 - right 데이터가 없을 때
    while len(left) > left_point:
        merged.append(left[left_point])
        left_point += 1
        
    # case3 - left 데이터가 없을 때
    while len(right) > right_point:
        merged.append(right[right_point])
        right_point += 1
    
    return merged

#split을 해준 뒤 merge 함수를 적절하게 넣어보자
def merge_sort(input):
    if len(input)<=1:
        return input
    
    medium = int(len(input)/2)
    left = merge_sort[:medium]
    right = merge_sort[medium:]
    
    return merge(left,right)

 

4. 의식의 흐름 정리

초반에 좀 해맸어서 어떤 의식의 흐름으로 코드를 완성했는지 좀 정리해볼까 합니다.

 

1)

일단 나눌 수 있는데까지 다 나눠야 하니까 나누는 함수 만들어 보자

def split(data):
    medium = int(len(data)/2)
    left = data[:medium]
    right = data[medium:]

 

2)

재귀적으로 원소 1개있을 때까지 나눠보자

def split(data):
    if len(data)<=1:
        print(1)
    
    medium = int(len(data)/2)
    left = split[:medium]
    right = split[medium:]

이런 느낌으로 짜고

마지막에 [left,right을 합쳐주면서 정렬까지 해주는 함수]를 넣어주면 좋지 않을까?

 

3)

left와 right를 합친 후, 정렬해주는 기능을 하는 merge(left, right) 함수를 만든 뒤

def merge_sort(data):
    if len(data) <= 1:
        return data
    medium = int(len(data) / 2)
    left = merge_sort(data[:medium])
    right = merge_sort(data[medium:])
    return merge(left, right)

이렇게 merge_sort(data) 함수를 짜주면 전체적으로 잘 작동합니다!

 

5. 시간 복잡도

• 정렬하려는 리스트의 길이가 8이면 3번 나눌 수 있으므로 depth는 3 --> 일반화하면 log n
• 각 단계별 계산 양 --> 결국에는 리스트를 여러개로 나누는 거니까 다 더하면 n
• 시간 복잡도는 O(n log n)